Застосування інтегралів

Приклад

Електровоз через t годин після відправлення мав прискорення a(t) = 3t² – 42t + 80 (км/год). Визначити швидкість і відстань, пройдену електровозом від станції через годину після відправлення, вважаючи v(0) = s (0) = 0.

♦ Нехай функція s(t) описує рух електровоза, а v(t) – його швидкість. Тоді, користуючись механічним змістом похідної та означенням первісної, розглядатимемо s(t) як одну з первісних для v(t), а v(t) – для a(t) на деякому проміжкузміни часу t. Оскільки за умовою задачі шукані величини потрібно обчислити за час t₁= 0 до t₂ = 1, то дістанемо:

v(t) = ∫ (3t² – 42 t + 80) dt = t³ – 21t² +80 t + C, де С = v (0) = 0.

Отже, v(t)= t³ – 21t² +80 t, v(1)= 1³ – 21·1² +80 ·1=60 км/ год, а

$s=\int_{0}^{1}{v(t)dt}=\int_{0}^{1}{(t^{3}-21t^{2}+80t)dt}=$

$=(\frac{t^{4}}{4}-7t^{3}+40t^{2})|_{0}^{1}=33,25$ км. ♦

Приклад

Знайти площу фігури, обмеженої лініями

$y^{2}-2y+x^{2}=0$ ,

$y^{2}-4y+x^{2}=0$ ,

$y=\frac{x}{\sqrt{3}}$ ,

$y=\sqrt{3}x$ .

♦ $(y^{2}-2y+1)-1+x^{2}=0$ ,

$(y-1)^{2}+x^{2}=1$ ,

$x^{2}+(y-1)^{2}=1$ – коло з центром в т. (0;1) і R = 1.

$(y^{2}-4y+4)-4+x^{2}=0$ ,

$(y-2)^{2}+x^{2}=4$ ,

$x^{2}+(y-2)^{2}=4$ – коло з центром в т. (0; 2) і R = 2.

Зобразимо графіки заданих кривих:

Перейдемо до полярних координат. За формулами переходу

$x=rcos\varphi, y=rsin\varphi$ .

Знайдемо полярні рівняння кіл:

$y^{2}-2y+x^{2}=0$ ,

$r^{2}sin^{2}\varphi -2rsin\varphi +r^{2}cos^{2}\varphi =0$ ,

$r^{2}(sin^{2}\varphi +cos^{2}\varphi )-2rsin\varphi =0$ ,

$r^{2}-2rsin\varphi =0$ ,

$r(r-2sin\varphi )=0$ ,

$r=2sin\varphi$ ;

$y^{2}-4y+x^{2}=0$ ,

$r^{2}sin^{2}\varphi -4rsin\varphi +r^{2}cos^{2}\varphi =0$ ,

$r^{2}(sin^{2}\varphi +cos^{2}\varphi )-4rsin\varphi =0$ ,

$r^{2}-4rsin\varphi =0$ ,

$r(r-4sin\varphi )=0$ ,

$r=4sin\varphi$ .

Отже, $2sin\varphi \leq r\leq 4sin\varphi$ .

Визначимо кут φ.

$y=\frac{x}{\sqrt{3}}$ ,

$k=\frac{1}{\sqrt{3}}\Rightarrow tg\varphi =\frac{1}{\sqrt{3}}\Rightarrow \varphi =30^{0}=\frac{\pi }{6}$ ,

$y=\sqrt{3}x$ ,

$k=\sqrt{3}\Rightarrow tg\varphi =\sqrt{3}\Rightarrow \varphi 60^{0}=\frac{\pi }{3}$ .

Отже, $\frac{\pi }{6}\leq \varphi \leq \frac{\pi }{3}$ .

Маємо: $S=\int \int _{D}dxdy=\int \int _{D}rdrd\varphi =$

$=\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}{d\varphi} \int_{2sin\varphi }^{4sin\varphi }{dr}=\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}{\frac{r^{2}}{2}}|_{2sin\varphi }^{4sin\varphi }d\varphi$

$=\frac{1}{2}\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}{\left(16sin^{2} \varphi -4sin^{2}\varphi \right)d\varphi }=$

$=\frac{1}{2}\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}12sin^{2}\varphi d\varphi =$

$=12\cdot \frac{1}{4}\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\left(1-cos2\varphi \right)d\varphi =$

$=3\left(\varphi -\frac{1}{2}sin2\varphi \right)|_{\frac{\pi }{6}}^{\frac{\pi }{3}}=$

$=3\left(\frac{\pi }{3} -\frac{1}{2}\cdot sin\frac{2\pi }{3}-\frac{\pi }{6}+\frac{1}{2}sin\frac{\pi }{3}\right)=$

$=\left(\frac{\pi }{6}-\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4} \right)=$

$=\frac{\pi }{3}\approx \frac{3,14}{3}\approx 1,04$ (кв. од.) ♦

Приклад

Обчислити площу фігури, обмеженої лініями

$y^{2}+4y+x^{2}=0$ ,

$y^{2}+8y+x^{2}=0$ ,

$y=-\frac{x}{\sqrt{3}}$ ,

$y=-x$ .

♦ Випадок аналогічний до попереднього прикладу. Cпочатку зобразимо фігуру, площу якої потрібно знайти.

Як і в попередньому випадку перейдемо до полярних координат, використовуючи формули переходу $x=rcos\varphi, y=rsin\varphi$ .

Спочатку запишемо рівняння першого кола в полярних координатах:

$y^{2}+4y+x^{2}=0,$

$\rho ^{2}sin^{2}\varphi +4\rho sin\varphi +\rho ^{2}cos^{2}\varphi =0,$

$\rho ^{2}+4\rho sin\varphi=0,$

$\rho (\rho +4sin\varphi )=0,$

$\rho =-4sin\varphi$

Друге коло в полярних координата запишеться аналогічно:

$y^{2}+8y+x^{2}=0,$

$\rho ^{2}sin^{2}\varphi +8\rho sin\varphi +\rho ^{2}cos^{2}\varphi =0,$

$\rho ^{2}+8\rho sin\varphi=0,$

$\rho (\rho +8sin\varphi )=0,$

$\rho =-8sin\varphi$

Отже, $-8sin\varphi \leq \rho \leq -4sin\varphi$ .

Визначимо, в яких межах буде знаходитися кут φ:

$y=-x\Rightarrow k=-1\Rightarrow tg\varphi =-1\Rightarrow \varphi =-45^{0}=-\frac{\pi }{4},$

$y=-\frac{x}{\sqrt{3}}\Rightarrow k=-\frac{1}{\sqrt{3}}\Rightarrow tg\varphi =-\frac{1}{\sqrt{3}}\Rightarrow \varphi =-30^{0}=-\frac{\pi }{6},$

Отже, $-\frac{\pi }{4}\leq \varphi \leq -\frac{\pi }{6}$ .

Тепер використаємо формулу для обчислення площі фігури через подвійний інтеграл, виконавши перехід до полярних координат:

$S=\int \int _{\phi }dxdy=\int \int _{\phi }\rho d\rho d\varphi =\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}d\varphi \int_{-4sin\varphi }^{-8sin\varphi}\rho d\rho \varphi =\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}d\varphi\frac{\rho ^{2}}{2}|_{-4sin\varphi }^{-8sin\varphi}=$

$=\frac{1}{2}\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}\left ( -16sin^{2}\varphi +64sin^{2}\varphi \right )d\varphi =24\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}sin^{2}\varphi d\varphi =$

$=24\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}\frac{1-cos2\varphi }{2} d\varphi =12\int_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}(1-cos2\varphi )d\varphi=12(\varphi -\frac{sin2\varphi }{2}) |_{-\frac{\pi }{4}}^{-\frac{\pi }{6}}=$

$=12(-\frac{\pi }{6}+\frac{\pi }{4}+\frac{sin\frac{\pi }{3}}{2}-\frac{sin\frac{\pi }{2}}{2})=12(\frac{-2\pi +3\pi }{12}+\frac{\sqrt{3}}{4}-\frac{1}{4})=$

$=12(\frac{\pi }{12}+\frac{\sqrt{3}-1}{4})=\pi +3\sqrt{3}-3$ (кв. од.) ♦

Приклад

Обчислити площу фігури, обмеженої лініями $x=y^{2}+2y-1,\; y=-1-x$

♦ $x=y^{2}+2y+1-2$

$x=\left(y+1 \right)^{2}-2$

$x+2=\left(y+1 \right)^{2}$

$y+1=\sqrt{x+2},\; x\geq -2$

$y=\sqrt{x+2}-1$

$\sqrt{x+2}-1=-1-x$

$\sqrt{x+2}=-x$

$x+2=x^{2}$

$x^{2}-x-2=0$

$x_{1}=-1,\; x_{2}=2$ – межі інтегрування.

$S=\int_{a}^{b}{\left(f_{1}\left(x \right) -f_{2}\left(x \right)\right)}dx=$

$=\int_{-1}^{2}{\left(\sqrt{x+2}-1+1+x \right)dx}=$

$=\left(\frac{2\sqrt{x+2}^{3}}{3}+\frac{x^{2}}{2} \right)|_{-1}^{2}=\frac{2\cdot 2^{3}}{3}+2-\frac{2}{3}-\frac{1}{2}=$

$=\frac{14}{3}+\frac{3}{2}=\frac{28+9}{6}=\frac{37}{6}=6\frac{1}{6}$ (кв. од.) ♦

Приклад

Знайти площу фігури, обмеженої лініями:

а) $2y=\sqrt{x}$ , $2xy=1$ , $x=16$ ;

б) $x^{2}+2x+y^{2}=0,\; y=0$ , $x^{2}+4x+y^{2}=0,\; y=\sqrt{3}x$ .

♦ а) Запишемо задані фунуції у явному вигляді: $y=\frac{\sqrt{x}}{2}$ , $y=\frac{1}{2x}$ .

Зобразимо фігуру, площу якої необхідно знайти:

Для обчислення площі використаємо подвійний інтеграл:

$S=\int \int _{\Phi }dxdy=\int_{1}^{16}{dx}\int_{\frac{1}{2x}}^{\frac{\sqrt{x}}{2}}{dy}=\int_{1}^{16}{dx}\left(\frac{\sqrt{x}}{2} -\frac{1}{2x}\right)=$

$=\frac{1}{2}\int_{1}^{16}{\left(\sqrt{x} \frac{1}{x}\right)dx}=\frac{1}{2}\left(\frac{x^{\frac{3}{2}}}{\frac{3}{2}}-ln\left|x \right| \right)|_{1}^{16}=$

$=\left(\frac{\sqrt{x}^{3}}{3}-ln\left|x \right| \right)|_{1}^{16}=\frac{4^{3}}{3}-ln16-\frac{1}{3}+ln1=$

$=\frac{64}{3}-\frac{1}{3}-ln16=21-ln16\approx 21-2,8=18,2$ (кв.од.).

б) Випадок аналогічний до прикладів, наведених вище.

Але спробуємо знайти площу фігури, не використовуючи переходу до полярних координат.

Визначимо вид кривих, що задані, використавши виділення повного квадрата:

$x^{2}+2x+1+y^{2}=1$ , $\left(x+1 \right)^{2}+y^{2}=1$ та $x^{2}+4x+4+y^{2}=4$ , $\left(x+2 \right)^{2}+y^{2}=2^{2}$ .

Це кола з центарми у точках (-1; 0), (-2; 0) та радіусами 1 і 2 відповідно. Зобразимо їх в системі координат:

Знайдемо точки перетину кола $x^{2}+2x+y^{2}=0$ з прямою $y=\sqrt{3}x$ :

$x^{2}+2x+\left(\sqrt{3}x \right)^{2}=0$ ,

$x^{2}+2x+3x^{2}=0$ ,

$4x^{2}+2x=0$ ,

$2x(2x+1)=0$ ,

$x_{1}=0,\; x_{2}=-0,5$ .

Використаємо подвійний інтеграл для обчислення площі отриманої фігури:

$S=\int \int _{\Phi }dxdy=\int_{-4}^{-2}{dx}\int_{-\sqrt{-x^{2}-4x}}^{0}{dy}+\int_{-2}^{-1}{dx}\int_{-\sqrt{-x^{2}-4x}}^{-\sqrt{-x^{2}-2x}}{dy}+$ ,

$+\int_{-1}^{-0,5}{dx}\int_{\sqrt{3}x}^{-\sqrt{-x^{2}-2x}}{dy}=$

$\int_{-4}^{-2}{dx}\int_{-\sqrt{-x^{2}-4x}}^{0}{dy}=\int_{-4}^{-2}{\sqrt{-x^{2}-4x}dx}=\int_{-4}^{-2}{\sqrt{4-\left(x+2 \right)^{2}}dx}=$ ,

$=\frac{x+2}{2}+\frac{2^{2}}{2}arcsin\frac{x+2}{2}|_{-4}^{-2}=0+2\cdot arcsin0-(-1)\cdot 0-2arcsin(-1)=$

$= 0+\pi =\pi$ ,

$\int_{-2}^{-1}{dx}\int_{-\sqrt{-x^{2}-4x}}^{-\sqrt{-x^{2}-2x}}{dy}=\int_{-2}^{-1}{\left(-\sqrt{-x^{2}-2x}+\sqrt{-x^{2}-4x} \right)dx}=$ ,

$=\int_{-2}^{-1}{\left( \sqrt{4-\left(x+2 \right)^{2}}-\sqrt{1-\left(x+2 \right)^{2}}\right)dx}=$ ,

$=\int_{-2}^{-1}\sqrt{4-\left(x+2 \right)^{2}}dx-\int_{-2}^{-1}\sqrt{1-\left(x+2 \right)^{2}}dx=$ ,

$=\left(\frac{x+2}{2}\sqrt{4-\left(x+2 \right)^{2}} +\frac{4}{2}arcsin\frac{x+2}{2}\right)|_{-2}^{-1}=$ ,

$=\frac{1}{2}\cdot \sqrt{3}+2\cdot arcsin\frac{1}{2}-0-2arcsin0-$ ,

$-\left(0\cdot \sqrt{0}+arcsin0+\frac{1}{1}\cdot \sqrt{0}-\frac{1}{2}arcsin\left(-1 \right) \right)=\frac{\pi }{4}$ ,

$\int_{-0,5}^{-1}{dx}\int_{\sqrt{3}x}^{-\sqrt{-x^{2}-2x}}{dy}=\int_{-0,5}^{-1}{\left(-\sqrt{-x^{2}-2x} -\sqrt{3}x\right)dx}=$ ,

$=-\int_{-0,5}^{-1}{\sqrt{1-\left(x+1 \right)^{2}}dx}-\sqrt{3}\int_{-0,5}^{-1}{xdx}=$ ,

$=\left(\frac{x+1}{1}\sqrt{1-\left(x+1 \right)^{2}}+\frac{1}{2}arcsin\frac{x+1}{1} \right)|_{-0,5}^{-1}-\sqrt{3}\cdot \frac{x^{2}}{2}|_{-0,5}^{-1}=$ ,

$=0+\frac{1}{2}arcsin0-\frac{1}{2}\cdot \frac{\sqrt{3}}{2}-\frac{1}{2}arcsin\frac{1}{2}-\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{8}=-\frac{5\sqrt{3}}{8}-\frac{\pi }{12}$ ,

$S=\pi +\frac{\pi }{4}-\frac{5\sqrt{3}}{8}-\frac{\pi }{12}=\frac{14\pi }{12}-\frac{5\sqrt{3}}{8}=\frac{7\pi }{6}-\frac{5\sqrt{3}}{8}\approx$ ,

$\approx 3,7-1,06=2,63$ . ♦

Приклад

Обчислити площу фігури, обмеженої графіками функцій y = 5sinx та y = 5cosx.

♦ Зобразимо графіки заданих функцій:

Знайдемо точки перетину кривих:

$5sinx=5cosx\; /:5cosx$

$\frac{sinx}{cosx}=1$

$tgx=1$

$x=\frac{\pi }{4}+\pi n,\; n\in Z$

Візьмемо $x_{1}=\frac{\pi }{4},\; n=0;$

$x_{2}=\frac{\pi }{4}+\pi =\frac{5\pi }{4},\; n=1.$

Оскільки потрібно обчислити площу фігури, яка складається із двох однакових частин, то можна визначити площу фігури на обраному проміжку і помножити на 2.

$S=2S_{n}$

$S_{n}=\int_{\frac{\pi }{4}}^{5\pi }{4}\left(5sinx-5cosx \right)dx=$

$=5\int_{\frac{\pi }{4}}^{5\pi }{4}\left(sinx-cosx \right)dx=5\left(-cosx-sinx \right)|_{\frac{\pi }{4}}^{\frac{5\pi }{4}}=$

$=5\left(-cos\frac{5\pi }{4}-sin\frac{5\pi }{4}+cos\frac{\pi }{4}+sin\frac{\pi }{4} \right)=$

$=5\left(-\left(-\frac{\sqrt{2}}{2} \right)-\left(-\frac{\sqrt{2}}{2} \right)+\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} \right)=$

$=5\cdot \frac{4\cdot \sqrt{2}}{2}=5\cdot 2\sqrt{2}=10\sqrt{2}$

$S=2\cdot 10\sqrt{2}=20\sqrt{2}$ (кв. од.)

Приклад

Знайти площу фігури, обмеженої лініями $\left\{\begin{matrix} x=8(t-sint);\\ y=8(1-cost), \end{matrix}\right.\; y=12,\; (0\leq x\leq 16\pi, y\geq 12)$

♦ Зобразимо фігуру, площу якої потрібно знайти:

Для обчислення площі фігури, заданої параметрично, використовуємо формулу:

$S=\int_{\alpha }^{\beta }{y(t)\left|x'(t) \right|dt}$ .

Знайдемо всі її складові:

$x'(t)=8-8cost,$

$y=8(1-cost),$

Визначимо верхню межу інтегрування, як точку перетину кривої і прямої:

$8(1-cost)\geq12,$

$1-cost\geq1,5,$

$cost=-0,5\Rightarrow t\in [-\frac{2\pi }{3}+2\pi n; \frac{2\pi }{3}+2\pi n], n\in Z$

Обчислимо шукану площу:

$S=\int_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}8(1-cost)\cdot 8(1-cost)dt=$

$=64\int_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}(1-cost)^{2}dt=$

$=64\int_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}(1-2cost+\frac{1+cos2t}{2})dt=$

$=64(t-2sint+\frac{1}{2}t+\frac{cos2t}{4})|_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}=$

$=64(\frac{3t}{2}-2sint+\frac{cos2t}{4})|_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}=$

$=(96t-128sint+16cos2t)|_{-\frac{2\pi }{3}}^{\frac{2\pi }{3}}=$

$=64\pi -128\cdot \sqrt{3}+16cos\frac{4\pi }{3}+64\pi -128\sqrt{3}-16cos\frac{4\pi }{3}=$

$=128(\pi -2\sqrt{3})$

Відповідь: кв. од.♦

Приклад

Знайти площу фігури, обмеженої лініями $\left\{\begin{matrix} x=2(t-sint);\\ y=2(1-cost), \end{matrix}\right.\; y=3,\; y\geq 3,\; 0\leq x\leq \pi$

♦ Аналогічно до попереднього прикладу:

$2(1-cost)=3\Rightarrow 1-cost=\frac{3}{2}$

$-cost=\frac{1}{2}$

$cost=-\frac{1}{2}$

$t=\frac{2\pi }{3}$

$S=\int_{\alpha }^{\beta }{y(t)\left|x'(t) \right|dt}=$

$= \int_{\frac{2\pi }{3}}^{\pi }{2(1-cost)(2-2cost)dt}=$

$=4\int_{\frac{2\pi }{3}}^{\pi }{(1-cost)(1-cost)dt}=$

$=4\int_{\frac{2\pi }{3}}^{\pi }{(1-cos^{2}t)dt}=4\int_{\frac{2\pi }{3}}^{\pi }{sin^{2}tdt}=$

$=4\int_{\frac{2\pi }{3}}^{\pi }{\frac{1-cos2t}{2}dt}=2\int_{\frac{2\pi }{3}}^{\pi }{\left(1-cos2t \right)dt}=$

$=2\left(t-\frac{sin2t}{2} \right)|_{\frac{2\pi }{3}}^{\pi }=$

$=2\left(\pi -\frac{sin2\pi }{2} -\frac{2\pi }{3}+\frac{sin\frac{4\pi }{3}}{2}\right)=$

$=2\left(\pi -0-\frac{2\pi }{3}+\frac{sin\frac{\pi }{3}}{2} \right)=$

$=2\left(\frac{\pi }{3}-\frac{\sqrt{3}}{4} \right)\approx 1,06$ (кв. од.) ♦

Приклад

Знайти площу фігури, заданої в полярній системі координат

$\rho =\frac{1}{2}+cos\varphi$

♦ $S=\frac{1}{2}\int_{\alpha }^{\beta }{\rho ^{2}(\varphi )d\varphi }=\frac{1}{2}\int_{0}^{2\pi } {\left(\frac{1}{2}+cos\varphi \right)^{2}d\varphi }=$

$=\frac{1}{2}\int_{0}^{2\pi }{\left(\frac{1}{4}+2cos\varphi +cos^{2} \varphi \right)d\varphi }=$

$=\frac{1}{2}\left(\frac{1}{4}\varphi +2sin\varphi \right)|_{0}^{2\pi }+\frac{1}{2}\int_{0}^{2\pi }{\frac{1+cos2\varphi }{2}d\varphi }=$

$=\frac{1}{2}\left(\frac{1}{1}\cdot 2\pi +2sin2\pi -0-0 \right)+\frac{1}{4}\left(\varphi +\frac{sin2\varphi }{2} \right)|_{0}^{2\pi }=$

$=\frac{1}{2}\cdot \frac{\pi }{2}+\frac{1}{4}\left(2\pi +0-0-0 \right)=$

$=\frac{\pi }{4}+\frac{\pi }{2}=\frac{3\pi }{4}\approx 2,4$ (кв. од.) ♦

Приклад

Обчислити площу плоскої фігури, обмеженої кривою $\rho =4sin^{2}\varphi$ . Побудувати задану криву.

♦ $\rho =4sin^{2}\varphi$ .

Зобразимо задану криву:

Використаємо формулу для обчислення площі фігури, обмеженої кривою, заданою в полярній системі координат:

$S=\frac{1}{2}\int_{\alpha }^{\beta }\rho ^{2}\left ( \varphi \right )d\varphi$

Визначимо межі інтегрування.Враховуючи те, що графік симетричний, можемо обчислювати площу на проміжку $\left [ 0;\frac{\pi }{2} \right ]$ , а потім помножити знайдене значення на 4.

$S_{1}=\frac{1}{2}\int_{0}^{\frac{\pi }{2}}\left ( 4sin^{2}\varphi \right )^{2}d\varphi =$

$=\frac{1}{2}\cdot 16\int_{0}^{\frac{\pi }{2}}sin^{4}\varphi d\varphi=8\int_{0}^{\frac{\pi }{2}}\left ( \frac{1-cos2\varphi }{2} \right )^{2}d\varphi =$

$=8\int_{0}^{\frac{\pi }{2}}\frac{1-2cos2\varphi +cos^{2}2\varphi }{4}d\varphi =$

$=2\int_{0}^{\frac{\pi }{2}}\left ( 1-2cos2\varphi +cos^{2}2\varphi \right )d\varphi=$

$=2\int_{0}^{\frac{\pi }{2}}\left ( 1-2cos2\varphi +\frac{1+cos4\varphi }{2} \right )d\varphi =$

$=2\int_{0}^{\frac{\pi }{2}}\left ( 1-2cos2\varphi +\frac{1}{2}+\frac{cos4\varphi }{2}\right )d\varphi=$

$=2\int_{0}^{\frac{\pi }{2}}\left ( \varphi -\frac{2sin2\varphi }{2}+\frac{1}{2}\varphi +\frac{sin4\varphi }{8} \right )|_{0}^{\frac{\pi }{2}}=$

$=2\left ( \frac{\pi }{2}-sin\pi +\frac{\pi }{4}+\frac{sin2\pi }{8}-0+sin0-0-sin0 \right )=$

$=2\left ( \frac{\pi }{2} +\frac{\pi }{4}\right )=2\cdot \frac{3\pi }{4}=\frac{3\pi }{2}$

$S=4S_{1}=4\cdot \frac{3\pi }{2}=6\pi$ ♦

Приклад

Знайти площу фігури, обмеженої заданою лінією $\left(x^{2}+y^{2} \right)^{2}=2a^{2}xy$ (лемніската Бернуллі). Зробити рисунок.

♦ Виконаємо перехід до полярних координат. Перехід від полярних до декартових координат здійснюється за формулами:

$\begin{cases} x=\rho cos\varphi , \\ y=\rho sin\varphi & \end{cases}.$ .

Підставивши ці рівності в задане рівняння кривої, отримаємо:

$\left(\rho ^{2}cos^{2}\varphi +\rho ^{2}sin^{2}\varphi \right)^{2}=2a^{2}\rho cos\varphi \cdot \rho sin\varphi ;$

$\left(\rho ^{2}\left( cos^{2}\varphi +sin^{2}\varphi \right) \right)^{2}=2a^{2}\rho ^{2}cos\varphi \cdot sin\varphi ;$

$\rho ^{4}=2a^{2}\rho ^{2}cos\varphi sin\varphi;\; |:\rho ^{2}$

$\rho ^{2}=2a^{2}cos\varphi sin\varphi;$

$\rho ^{2}=a^{2}2cos\varphi sin\varphi;$

$\rho ^{2}=a^{2} sin2\varphi;$

$\rho =a\sqrt{sin2\varphi }$ .

Знайдемо як зміниться кут:

$sin2\varphi \geq 0\Rightarrow 2\pi k\leq 2\varphi \leq \pi +2\pi k,\; k\in Z,$

$\pi k\leq \varphi \leq \frac{\pi }{2}+\pi k,\; k\in Z$ .

Користуючись симетрією лемніскати, знайдемо шукану площу S=4S₁, де S₁ – це площа фігури, що міститься в куті $\text{[math]}$ за формулою:

$S=4S_{1}=4\cdot \frac{1}{2}\int_{\alpha }^{\beta }{\rho^{2} \left(\varphi \right)d\varphi }=$

$=2\int_{0}^{\frac{\pi }{4}}{a^{2}sin2\varphi d\varphi }=2a^{2}\cdot \frac{-cos2\varphi }{2}|_{0}^{\frac{\pi }{4}}=$

$=-a^{2}cos2\varphi |_{0}^{\frac{\pi }{4}}=-a^{2}\left(cos\frac{\pi }{2}-cos0 \right)=$

$=-a^{2}\left(0-1 \right)=-a^{2}\cdot \left(-1 \right)=a^{2}$ .

♦

Приклад

Обчислити площу фігури, обмеженої кривою

r = 6sin3φ, r = 3 (r ≥ 3).

♦ Побудуємо графіки заданих кривих в полярній системі координат. Перша функція задає трипелюсткову троянду, друга – коло, радіуса 3.

Площа шуканої фігури складається з трьох однакових частин. Тому, обчислимо площу однієї частини і помножимо на три.

$S_{1}=\frac{1}{2}\int_{\alpha }^{\beta }{\left(r_{2} ^{2}\left(\varphi \right)-r_{1}^{2}\left(\varphi \right)\right)d\varphi }=$

$=\frac{1}{2}\int_{0}^{\frac{\pi }{3}}{\left(\left(6sin3\varphi \right)^{2}-3^{2} \right)d\varphi }=\frac{1}{2}\int_{0}^{\frac{\pi }{3}}{\left(36sin^{2}3\varphi -9 \right)d\varphi }=$

$=\frac{9}{2}\int_{0}^{\frac{\pi }{3}}{\left(4sin^{2}3\varphi -1 \right)d\varphi }=\frac{9}{2}\int_{0}^{\frac{\pi }{3}}{\left(4\cdot \frac{1-cos6\varphi }{2}-1 \right)d\varphi }=$

$=\frac{9}{2}\int_{0}^{\frac{\pi }{3}}{\left(2-2cos6\varphi -1 \right)d\varphi }=\frac{9}{2}\int_{0}^{\frac{\pi }{3}}{\left(1-2cos6\varphi \right)d\varphi }=$

$=\frac{9}{2}\left(\varphi -\frac{2sin6\varphi }{6} \right)|_{0}^{\frac{\pi }{3}}=\frac{9}{2}\left(\varphi -\frac{sin6\varphi }{3} \right)|_{0}^{\frac{\pi }{3}}=$

$=\frac{9}{2}\left(\frac{\pi }{3}-\frac{sin2\pi }{3}-0+sin0 \right)=\frac{9}{2}\cdot \frac{\pi }{3}=\frac{3\pi }{2}$ (кв. од.)

$S=3S_{1}=3\cdot \frac{3\pi }{2}=\frac{9\pi }{2}=4,5\pi$ (кв. од.)♦

Приклад

Обчислити площу фігури, обмеженої кривими

r = 2cosφ, r = 3cosφ.

♦ Зобразимо площу, обмежену заданими кривимим:

$S=\frac{1}{2}\int_{\alpha }^{\beta }(\rho _{2}^{2}(\varphi )-\rho _{1}^{2}(\varphi ))$

$S=\frac{1}{2}\int_{0}^{2\pi }(9cos^{2}\varphi -4cos^{2}\varphi )d\varphi =\frac{1}{2}\int_{0}^{2\pi }5cos^{2}\phi d\varphi =$

$=2,5\int_{0}^{2\pi }\frac{1+cos2\varphi }{2}d\varphi =1,25\int_{0}^{2\pi }(1+cos2\varphi )d\varphi =$

$=1,25(\varphi +\frac{sin2\varphi }{2})|_{0}^{2\pi }=1,25(2\pi +0-0-0)=2,5\pi$

Відповідь: $2,5\pi$ ♦

Приклад

Ріка тече лугом, утворюючи криву у = х – х²; вісь Ох – лінія шосе. Яка площа лугу між шосе та річкою (одиниця довжини 1 км)

♦

За формулою $S=\int_{a}^{b}{f(x)dx}$ , де f(x) = x – x², a=0, b = 1 маємо $S =\int_{0}^{1}{(x-x^{2}) dx} = \left(\frac{x^{2}}{2}-\frac{x^{3}}{3} \right)|_{0}^{1}=\frac{1}{6}$ км². Оскільки 1 га = 0,01 км², то S = 16,67 га.♦

Приклад

Обчислити площу лунки, обмеженої дугами кіл ρ = sin φ i ρ = cos φ, 0 ≤ φ ≤ π/2.

♦ Визначимо полярну координату φ точки перетину даних кіл із системи рівнянь.

Маємо sin φ = cos φ, tg φ = 1, φ = arctg 1 = π/4.

Площа S даної фігури дорівнює сумі площ S₁ і S₂ криволінійних секторів OnM i OmM. Оскільки ці площі рівні між собою, то досить обчислити одну з них, наприклад S_1.

Дуга OnM описується кінцем полярного радіуса ρ кола ρ = sin φ при зміні полярного кута від α = 0 до α = π/4. Тому, використовуючи формулу $S=\frac{1}{2}\int_{\alpha }^{\beta }{(\rho _{2}^{2}(\varphi )-\rho _{1}^{2}(\varphi ))d\varphi }$ , знаходимо

$S_{1}=\frac{1}{2}\int_{0}^{\frac{\pi }{4}}{\rho ^{2}d\varphi }=\frac{1}{2}\int_{0}^{\frac{\pi }{4}}{sin^{2}\varphi d\varphi }=$

$=\frac{1}{4}\int_{0}^{\frac{\pi }{4}}{(1-cos\varphi )d\varphi }=\frac{1}{4}(\varphi -\frac{1}{2}sin2\varphi )|_{0}^{\frac{\pi }{4}}=\frac{1}{16}(\pi -2)$ .

Отже, $S=2S_{1}=\frac{1}{8}(\pi -2)$ . ♦

Приклад

Знайти довжину дуги кривої $y=lnx$ , при $\frac{3}{4}\leq x\leq \frac{12}{5}$ .

♦ Зобразимо дану криву:

Довжину дуги кривої обчислимо за формулою:

$=\int_{a}^{b}{\sqrt{1+y'^{2}}dx}=\int_{\frac{3}{4}}^{\frac{12}{5}}{\sqrt{1+\left(\frac{1}{x} \right)^{2}}dx}=\int_{\frac{3}{4}}^{\frac{12}{5}}{\sqrt{1+\frac{1}{x^{2}}}dx}=$

$=\int_{\frac{3}{4}}^{\frac{12}{5}}{\frac{\sqrt{x^{2}+1}}{x}dx}=\int_{\frac{3}{4}}^{\frac{12}{5}}{x^{-1}\left(1+x^{2} \right)dx}=\begin{vmatrix} m=-1\\ n=2\\ \frac{m+1}{n}=\frac{-1+1}{2}=0\in Z \end{vmatrix}$ .

Виконаємо підстановку:

$1+x^{2}=t^{2},$

$x^{2}=t^{2}-1,$

$x=\sqrt{t^{2}-1}$ .

Звідси, $dx=\frac{1}{\sqrt{t^{2}-1}}\cdot 2tdt=\frac{tdt}{\sqrt{t^{2}-1}}$ .

Знайдемо $t_{1}=\sqrt{x_{1}^{2}+1}=\sqrt{\left(\frac{3}{4} \right)^{2}+1}=\sqrt{\frac{9}{16}+1}=\sqrt{\frac{25}{16}}=\frac{5}{4}$

$t_{2}=\sqrt{x_{2}^{2}+1}=\sqrt{\left(\frac{12}{5} \right)^{2}+1}=\sqrt{\frac{144}{25}+1}=\sqrt{\frac{169}{25}}=\frac{13}{5}$ .

Підставивши всі знайдені значення в інтеграл, отримаємо:

$=\int_{\frac{5}{4}}^{\frac{13}{5}}{\frac{\sqrt{t^{2}}}{\sqrt{t^{2}-1}}}\cdot \frac{tdt}{\sqrt{t^{2}-1}}=\int_{\frac{5}{4}}^{\frac{13}{5}}{\frac{t\cdot tdt}{t^{2}-1}}=$

$=\int_{\frac{5}{4}}^{\frac{13}{5}}{\frac{t^{2}dt}{t^{2}-1}}=\int_{\frac{5}{4}}^{\frac{13}{5}}{\frac{\left(t^{2} -1\right)+1}{t^{2}-1}dt}=$

$=\int_{\frac{5}{4}}^{\frac{13}{5}}{\left(1 +\frac{1}{t^{2}-1}\right)dt}=\int_{\frac{5}{4}}^{\frac{13}{5}}{dt}+\int_{\frac{5}{4}}^{\frac{13}{5}}{\frac{dt}{t^{2}-1}}=$

$=t|_{\frac{5}{4}}^{\frac{13}{5}}+\frac{1}{2}ln\left|\frac{t-1}{t+1} \right||_{\frac{5}{4}}^{\frac{13}{5}}=\frac{13}{5}-\frac{5}{4}+\frac{1}{2}ln\left|\frac{\frac{13}{5}-1}{\frac{13}{5}+1} \right|-$

$-\frac{1}{2}ln\left|\frac{\frac{5}{4}-1}{\frac{5}{4}+1} \right|=\frac{52-25}{20}+\frac{1}{2}ln\left|\frac{\frac{8}{2}}{\frac{18}{5}} \right|-\frac{1}{2}ln\left|\frac{\frac{1}{4}}{\frac{9}{4}} \right|=$

$=\frac{27}{20}+\frac{1}{2}ln\frac{4}{9}-\frac{1}{2}ln\frac{1}{9}=\frac{27}{20}-\frac{1}{2}ln\frac{\frac{4}{9}}{\frac{1}{9}}=$

$=\frac{27}{20}-\frac{1}{2}ln4=\frac{27}{20}-ln\sqrt{4}=\frac{27}{20}-ln2$ .♦

Приклад

Знайти довжину дуги кривої $y=1+arcsinx -\sqrt{1-x^{2}}$ , при $0\leq x\leq \frac{3}{4}$ .

♦ Зобразимо криву, довжину якої потрібно знайти:

Довжину дуги кривої обчислимо за формулою:

$l=\int_{a}^{b}\sqrt{1+f'^{2}(x)}dx,$

$y'=\frac{1}{\sqrt{1-x^{2}}}+\frac{x}{\sqrt{1-x^{2}}}=\frac{1+x}{\sqrt{1-x^{2}}},$

$l=\frac{0}{\frac{3}{4}}\sqrt{1+\frac{(1+x)^{2}}{1-x^{2}}}dx=\int_{0}^{\frac{3}{4}}\sqrt{\frac{1-x^{2}+1+2x+x^{2}}{1-x^{2}}}dx=$

$=\frac{0}{\frac{3}{4}}\sqrt{\frac{2+2x}{1-x^{2}}}dx=\frac{0}{\frac{3}{4}}\sqrt{\frac{2(1+x)}{(1+x)(1-x)}}dx=$

$=\sqrt{2}\frac{0}{\frac{3}{4}}\frac{dx}{\sqrt{1-x}}=\begin{vmatrix} 1-x=t,\\ -dx=dt,\\ dx=-dt \end{vmatrix}=-\sqrt{2}\frac{0}{\frac{3}{4}}\frac{dt}{\sqrt{t}}=-\sqrt{2}\frac{0}{\frac{3}{4}}t^{-\frac{1}{2}}dt=$

$=-\sqrt{2}\cdot \frac{t^{\frac{1}{2}}}{\frac{1}{2}}|_{0}^{\frac{3}{4}}=-2\sqrt{2}(\sqrt{\frac{1}{4}}-\sqrt{1})=-2\sqrt{2}\cdot (-\frac{1}{2})=\sqrt{2}$

Відповідь: $\sqrt{2}$ ♦

Приклад

Обчислити довжину кардіоїди ρ = 1 + cos φ

♦ Зобразимо задану криву:

Задана крива симетрична відносно полярної осі, тому при зміні кута φ від 0 до π полярний радіус опише половину кривої. Обчислюємо довжину заданої кривої за формулою $l=\int_{\alpha }^{\beta }{\sqrt{x'^{2}(t)+y'^{2}(t)}dt}$ , враховуючи, що ρ’ = – sin φ:

$l=2\int_{0}^{\pi }{\sqrt{(1+cos \varphi )^{2}+sin^{2}\varphi }d\varphi }=2\int_{0}^{\pi }{2(1+cos\varphi )d\varphi }=$

$=4\int_{0}^{\pi }{cos\frac{\varphi }{2}d\varphi }=8sin\frac{\varphi }{2}|_{0}^{\pi }=8$ ♦

Приклад

Обчислити довжину дуги, обмеженої кривою r = 3φ, якщо $0\leq \varphi \leq \frac{4}{3}$ .

♦ Маємо спіраль Архімеда. Зобразимо перший виток цієї кривої:

Довжина дуги кривої, заданої параметрично, обчислюється за формулою $l=\int_{\alpha }^{\beta }\sqrt{\rho ^{2}(\varphi )+\rho' ^{2}(\varphi )}d\varphi$ .

$l=\int_{\alpha }^{\beta }\sqrt{\rho ^{2}(\varphi )+\rho' ^{2}(\varphi )}d\varphi =\int_{0}^{\frac{4}{3}}\sqrt{9\varphi ^{2}+9}d\varphi =$

$=3\int_{0}^{\frac{4}{3}}\sqrt{1+\varphi ^{2}}d\varphi =3(\frac{\varphi }{2}\sqrt{1+\varphi ^{2}}+\frac{1}{2}ln(\varphi +\sqrt{1+\varphi ^{2}}))|_{0}^{\frac{4}{3}}=$

$=3(\frac{3}{8}\sqrt{1+\frac{9}{16}}+\frac{1}{2}ln(\frac{3}{4})\sqrt{1+\frac{9}{16}}-0-\frac{1}{2}ln1)=$

$=3(\frac{3}{8}\cdot \frac{5}{4}+\frac{1}{2}ln(\frac{3}{4}+\frac{5}{4})-0-0)=$

$=3(\frac{15}{32}+\frac{1}{2}ln2)=\frac{45}{32}+\frac{3}{2}ln2=\frac{45}{32}+ln\sqrt{8}$

Відповідь: $\frac{45}{32}+ln\sqrt{8}$ ♦

Приклад

Обчислити довжину дуги, обмеженої кривою r = 6φ.

♦ Випадок аналогічний до попереднього прикладу. Зобразимо перший виток заданої спіралі Архімеда:

Довжину дуги кривої, заданої в полярній системі координат, обчислимо за формулою:

$l=\int_{\alpha }^{\beta }{\sqrt{r^{2}\left(\varphi \right)+r'^{2}\left(\varphi \right)}d\varphi }=$

$=\int_{0}^{2\pi }{\sqrt{\left(6\varphi \right)^{2}+6^{2}}d\varphi }=\int_{0}^{2\pi }{\sqrt{36\varphi ^{2}+36}d\varphi }=$

$=6\int_{2}^{2\pi }{\sqrt{\varphi ^{2}+1}d\varphi }=\begin{vmatrix} U=\sqrt{\varphi ^{2}+1} & dV=d\varphi \\ dU=\frac{\varphi d\varphi }{\sqrt{\varphi ^{2}+1}} & V=\varphi \end{vmatrix}=$

$=6\left(\varphi \sqrt{\varphi ^{2}+1}|_{0}^{2\pi }-\int_{0}^{2\pi }{\frac{\varphi ^{2}d\varphi }{\sqrt{\varphi ^{2}+1}}} \right)=$

$=6\left(2\pi \sqrt{4\pi ^{2}+1} -0\right)-6\int_{0}^{2\pi }{\frac{\left(\varphi ^{2}+1 \right)-1}{\sqrt{\varphi ^{2}+1}}}=$

$=12\pi \sqrt{4\pi ^{2}+1}-6\int_{0}^{2\pi }{\sqrt{\varphi ^{2}+1}}+6\int_{0}^{2\pi }{\frac{d\varphi }{\varphi ^{2}+1}}\Rightarrow$

$\Rightarrow 12\int_{0}^{2\pi }{\sqrt{\varphi ^{2}+1}d\varphi }=12\pi \sqrt{4\pi ^{2}+1}+6ln\left(\varphi +\sqrt{\varphi ^{2}+1} \right)|_{0}^{2\pi }\Rightarrow$

$\Rightarrow 6\int_{0}^{2\pi }{\sqrt{\varphi ^{2}+1}d\varphi }=6\pi \sqrt{4\pi ^{2}+1}+3ln\left(2\pi +\sqrt{4\pi ^{2}+1} \right)-$

$-6ln\left(0+\sqrt{0+1} \right)=6\pi \sqrt{4\pi ^{2}+1}+3ln\left(2\pi +\sqrt{4\pi ^{2}+1} \right)-6ln1=$

$=6\pi \sqrt{4\pi ^{2}+1}+3ln\left(2\pi +\sqrt{4\pi ^{2}+1} \right)$ .♦

Приклад

Знайти довжину дуги кривої, заданої параметрично $\left\{\begin{matrix} x=e^{t}(cost+sint);\\ y=e^{t}(cost-sint) \end{matrix}\right.$ , при $0\leq t\leq \frac{3\pi }{2}$ .

♦ Довжина дуги, заданої параметрично, обчислюється за формулою:

$l=\int_{\alpha }^{\beta }\sqrt{x'^{2}(t)+y'^{2}(t)}dt,$

$x'(t)=e^{t}(cost+sint)+e^{t}(-sint+cost)=$

$=e^{t}\cdot 2cost=2e^{t}\cdot cost;$

$y'(t)=e^{t}(cost-sint)+e^{t}(-sint-cost)=$

$=e^{t}\cdot (-2sint)=-2e^{t}\cdot sint$ .

$l=\int_{0}^{\frac{3\pi }{2}}\sqrt{4e^{2t}cos^{2}t+4e^{2t}sin^{2}t}dt=$

$=\int_{0}^{\frac{3\pi }{2}}2e^{t}dt=2e^{t}|_{0}^{\frac{3\pi }{2}}=2e^{\frac{3\pi }{2}}-2\cdot e^{0}=2e^{\frac{3\pi }{2}}-2$

Відповідь: $2e^{\frac{3\pi }{2}}-2$ ♦

Приклад

Обчислити площу поверхні обертання навколо осі Ох однієї арки циклоїди

x = t – sin t, y = 1 – cos t

♦ За формулою для параметрично заданої функції $P = 2\pi \int_{a}^{b}{\left|f(x) \right|\sqrt{1+f'^{2}(x)}dx}$ дістаємо

$P = 2\pi \int_{0}^{2\pi }{(1-cos t)\sqrt{(1-cost)^{2}+sin^{2}t}dt}=8\pi \int_{0}^{2\pi }{sin^{3}\frac{t}{2}dt}=$

$=8\pi \int_{0}^{2\pi }{(sin\frac{t}{2}-cos^{2}\frac{t}{2}sin\frac{t}{2})dt}=8\pi (-2cos\frac{t}{2}-\frac{2}{3}cos^{3}\frac{t}{2})|_{0}^{2\pi }=$

$=\frac{64}{3}\pi$ .♦

Приклад

Пластинка D задана кривими, які її обмежують. γ – поверхнева густина. Знайти масу пластинки.

D: x²= 4y, x = 0

y = 1 (x ≥ 0)

γ = x + 5y²

y = 4/x²

♦ Зобразимо на графіку криві, які обмежують задану пластинку.

Використовуючи формулу для обчислення маси через подвійний інтеграл, запишемо:

$m = \int \int _{D}\gamma (x;y)dxdy=\int \int _{D_{1}}\gamma (x;y)dxdy+\int \int _{D_{2}}\gamma (x;y)dxdy=$

$=\int_{1}^{+\infty}{dy}\int_{0}^{2\sqrt{y}}{\left(x+5y^{2} \right)dx}+\int_{2}^{+\infty}{dx}\int_{\frac{4}{x^{2}}}^{1}{\left(x+5y^{2} \right)dy}=I_{1}+I_{2}$

$I_{1}=\int_{1}^{+\infty}{dy}\int_{0}^{2\sqrt{y}}{\left(x+5y^{2} \right)dx}=\int_{1}^{+\infty}{dy\left(x^{2}+5xy^{2} \right)}|_{0}^{2\sqrt{y}}=$

$=\int_{1}^{+\infty}{\left(4y+5\sqrt{y}\cdot y^{2} \right)dy}=\left(\frac{4y^{2}}{2}+\frac{2\cdot 5\cdot y^{\frac{7}{2}}}{7} \right)|_{1}^{\infty}=$

$=2y^{2}+\frac{10}{7}y^{\frac{7}{2}}|_{1}^{\infty}=\lim_{b\rightarrow +\infty}\left(2b^{2}+\frac{10}{7}b^{3}\sqrt{b}-2 -\frac{10}{7}\right)=\infty$

$I_{2}=\int_{2}^{+\infty}{dx}\int_{\frac{4}{x^{2}}}^{1}{\left(x+5y^{2} \right)dy}=\int_{2}^{+\infty}{\left(xy+\frac{5y^{3}}{3} \right)}|_{\frac{4}{x^{2}}}^{1}=$

$=\int_{2}^{+\infty}{\left(x+\frac{5}{3}-\frac{4}{x}-\frac{5}{3}\cdot \frac{64}{x^{6}} \right)dx}=$

$=\left(\frac{x^{2}}{2}+\frac{5}{3}x-4ln\left|x \right|-\frac{320}{3}\cdot \frac{1}{-5x^{5}} \right)|_{2}^{+\infty}=$

$=\lim_{b\rightarrow \infty}\left(\frac{b^{2}}{2}+\frac{5}{3}b-4ln\left|b \right| +\frac{64}{3b^{5}}-2-\frac{10}{3}+4ln2-\frac{64}{3\cdot 32}\right)=$

$=\lim_{b\rightarrow \infty}\left(\frac{b^{2}}{2}+\frac{5b}{3}-4ln\left|b \right| +\frac{64}{3b^{5}}+4ln2-6\right)=\infty$

$m=I_{1}+I_{2}=\infty+\infty=\infty$ ♦

Приклад

Обчислити об’єм тіла, утвореного обертанням навколо осі Оу криволінійної трапеції $y^{2}=4-x, x=0$ . Зробити схематичний рисунок.

♦ Зобразимо задане тіло.

Використаємо формулу для обчислення об’єму тіла обертання: $V=\pi \int_{a}^{b}f^{2}(x)dx$ .

$V=\pi \int_{-4}^{4}\left ( 4-x \right )dx=\pi \left ( 4x-\frac{x^{2}}{2} \right )|_{-4}^{4}=$

$=\pi \left ( 16-\frac{16}{2}+16+ \frac{16}{2}\right )=32\pi$ .♦

Приклад

Обчислити об’єм тіла, утвореного обертанням навколо осі Оу криволінійної трапеції $y^{2}=x-2, y=0, y=x^{3}, y=1$ . Зробити схематичний рисунок.

♦ Зобразимо задане тіло.

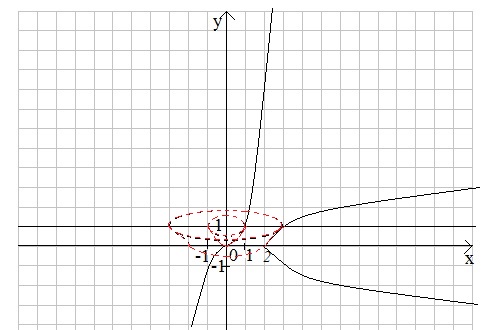
Об'єм тіла обертання — Об’єм тіла обертання

Як і в попередньому прикладі, використаємо формулу:

$V=\pi \int_{a}^{b}(f_{2}^{2}(y)-f_{1}^{2}(y)))dy,$

$f_{1}(y)=\sqrt[3]{y}, f_{2}(y)=y^{2}+2,$

$V=\pi \int_{0}^{1}((y^{2}+2)^{2}-\sqrt[3]{y^{2}})dy=$

$=\pi \int_{0}^{1}(y^{4}+4y^{2}+4-y^{\frac{2}{3}})dy=\pi (\frac{y^{5}}{5}+\frac{4y^{3}}{3}+4y-\frac{y^{\frac{5}{3}}}{\frac{5}{3}})|_{0}^{1}=$

$=\pi (\frac{y^{5}}{5}+\frac{4y^{3}}{3}+4y-\frac{3y^{\frac{5}{3}}}{5})=$

$=\pi (\frac{1}{5}+\frac{1}{3}+4-\frac{3}{5}-0)=\pi (4+\frac{1}{3}-\frac{2}{5})=$

$=\pi \cdot \frac{60+5-6}{15}=\frac{59\pi }{15}$

Відповідь: $\frac{59\pi }{15}$ (куб. од.)♦

Приклад

Визначити об’єм діжки за розмірами перерізу, вказаного на малюнку, де верхня і нихня криві – параболи y = ±px² ± q. Обчислити цей об’єм при r = 0,75 м, R = 1 м та l = 3 м.

♦ Скористаємося формулою $V=\pi \int_{a}^{b}{f^{2}(x)dx}$ , де f(x) = -px² + q – рівняння верхньої параболи, а = -l/2, q = l/2.

Спочатку знайдемо загальну формулу для обчислення об’єму діжки як тіла обертання, враховуючи її симетричність відносно осі OY. Маємо:

$\frac{1}{2}V=\pi \int_{0}^{\frac{l}{2}}{(-px^{2}+q)^{2}dx}=\pi \int_{0}^{\frac{l}{2}}{(p^{2}x^{4}-2pqx^{2}+q^{2})dx}=$

$=\pi (\frac{p^{2}}{5}x^{5}-\frac{2}{3}pqx^{3}+q^{2}x)|_{0}^{\frac{l}{2}}=\frac{\pi }{15}(\frac{3}{32}p^{2}l^{5}-\frac{5}{4}pql^{3}+\frac{15}{2}q^{2}l)$

Тоді

$V = \frac{\pi }{15\cdot 16}((3p^{2}l^{5}-40pql^{3}+15\cdot 16q^{2}l)$

Оскільки y = R при x = 0 і y = r при x = l / 2, то q = R і $p=\frac{4(R-r)}{l^{2}}$ , тобто рівняння верхньої параболи має вигляд $y=\frac{4(r-R)}{l^{2}}x^{2}+R$ . Отже,

$V=\frac{\pi l}{15}(3(R-r)^{2}-10R(R-r)+15R^{2})=\frac{\pi l}{15}(8R^{2}+4Rr+3r^{2})$

При заданих значеннях r = 0,75 м, R = 1 м та l = 3 м. дістанемо V = 2,54 π ≈ 8 м³. ♦

Приклад

Знайти подвійним інтегруванням об’єм тіла, обмеженого заданими поверхнями:

$3x+4y+z=12$ , $x^2+4y^2=4, \; z=1$ .

♦ $\frac{x^{2}}{4}+y^{2}=1$ – еліпс.

$V=\int \int _{D}(1-3x-4y)dxdy=$

$=\int_{-2}^{2}{dx}\int_{-1}^{1}{(11-3x-4y)dy}=$

$=\int_{-2}^{2}{dx}(11y-3xy-\frac{4y^{2}}{2})|_{-1}^{1}=$

$=\int_{-2}^{2}{(11-3x-2+11-3x+2)dx}=$

$=\int_{-2}^{2}{(22-6x)dx}=(22x-3x^{2})|_{-2}^{2}=$

$=22\cdot 2-3\cdot 4+22\cdot 2+3\cdot 4=44+44=88$ (куб. од.) ♦

Приклад

Знайти середнє значення функції U = U(x; y; z) в заданній області V:

$U = y^{2}zcos(\frac{1}{3}xyz)$ ,

$V: \begin{matrix} z = 2\pi, & y=1, & x=3\\ z=0, & y=0, & x=0 \end{matrix}$ .

♦ $U_{c}=\frac{1}{V}\int \int \int _{V}U(x,y,z)dxdydz$ ,

$V=2\pi \cdot 1\cdot 3=6\pi$ (куб. од.),

$U_{c}=\frac{1}{6\pi }\int_{0}^{1}{dy}\int_{0}^{2\pi }{dz}\int_{0}^{3}{y^{2}zcos(\frac{1}{3}xyz)dx} =$ ,

$=\frac{1}{6\pi }\int_{0}^{1}{dy}\int_{0}^{2\pi }{dz}\left(y^{2}z\frac{sin\left(\frac{1}{3}xyz \right)}{\frac{1}{3}yz} \right)|_{0}^{3}=$ ,

$=\frac{1}{6\pi }\int_{0}^{2\pi }{dz\left(3ysin\left(yz \right) \right)}=$ ,

$=\frac{1}{6\pi }\int_{0}^{1}{dy}\int_{0}^{2\pi }{3ysin\left(yz \right)dz}=$ ,

$=\frac{1}{6\pi }\int_{0}^{1}{dy}\cdot 3y\cdot \frac{-cos(yz)}{y}|_{0}^{2\pi }=$ ,

$=\frac{1}{2\pi }\int_{0}^{1}{\left(-cos(2\pi y)+1 \right)dy}=$ ,

$=\frac{1}{2\pi }\left(y-\frac{sin2\pi y}{2\pi } \right)|_{0}^{1}=$ ,

$=\frac{1}{2\pi }\left(1-\frac{sin2\pi }{2\pi }-0+\frac{sin0}{2\pi } \right)=\frac{1}{2\pi }$ (куб. од.)♦

Приклад

Знайти роботу сили F при переміщенні вздовж лінії L від точки М до точки N:

$\bar{F}=(x+y)\bar{i}+(x-y)\bar{j}$ ,

$L:y=x^{2}$ ,

$M(-1;1),\; N(1;1)$ .

♦ $W=\int _{MN}Pdx+Qdy=\int _{MN}\left(x+y \right)dx+\left(x-y \right)dy=$

$=\int_{-1}^{1}{\left(x+x^{2} \right)dx}+\int_{1}^{1}{\left(\sqrt{y}-y \right)dy}=$

$=\left(\frac{x^{2}}{2}+\frac{x^{3}}{3} \right)|_{-1}^{1}+\left(\frac{2\sqrt{y^{3}}}{3}-\frac{y^{2}}{2} \right)|_{1}^{1}=$

$=\frac{1}{2}+\frac{1}{3}-\frac{1}{2}+\frac{1}{3}+\frac{2}{3}-\frac{1}{2}-\frac{2}{3}+\frac{1}{2}=\frac{2}{3}$ .♦

Приклад

Обчислити циркуляцію вектора а по контуру L

а) безпосередньо; б) за формулою Стокса.

$\vec{a}=y\vec{i}+3x\vec{j}+z^{2}\vec{k}$

$L: \left\{\begin{matrix} z=x^{2}+y^{2}-1,\\ z=3. \end{matrix}\right.$

♦ а) За формулою Стокса:

$\int _{L_{\Pi }^{+}}Pdx+Qdy+Rdz=$

$=\int \int _{S^{+}}(R^{'}_{y}-Q^{'}_{z})dydz+(P^{'}_{z}-R^{'}_{x}dxdz+(Q^{'}_{x}-P^{'}_{y})dxdy$

$P=y,\; Q=3x,\; R=z^{2}$

$\begin{matrix} R^{'}_{y}=0 & R^{'}_{x}=0\\ Q^{'}_{z}=0 & Q^{'}_{x}=3\\ P^{'}_{z}=0 & P^{'}_{y}=1 \end{matrix}$

Ц = $\int \int _{S}=(3-1)dxdy=2\int \int _{D}dxdy=$

$=2\int_{0}^{2\pi }{d\varphi }\int_{0}^{1}{\rho d\rho }=2\cdot 2\pi \cdot \frac{1}{2}=2\pi$ .

б) Безпосередньо:

Ц = $\int _{L}Pdx+Qdy+Rdz=$

$=\int ydx+\int 3xdy+\int z^{2}dz=$

$\begin{matrix} x=cost & y=sint & z=cos^{2}t+sin^{2}t-1=1-1=0 \\ dx=-sintdt & dy=costdt & dz=0 \end{matrix}$

$= \int_{0}^{2\pi }{sint\cdot \left(-sint \right)dt}+\int_{0}^{2\pi }{3cost\cdot costdt}+0=$

$=\int_{0}^{2\pi }{\left(3cos^{2}t-sin^{2}t \right)dt}=$

$=\frac{1}{2}\int_{0}^{2\pi }{\left(3+3cos2t-1+cos2t \right)dt}=$

$=\int_{0}^{2\pi }{\left(1+2cos2t \right)dt}=\left(t+\frac{2sin2t}{2} \right)|_{0}^{2\pi }=2\pi$ . ♦

Приклад

Знайти похідну скалярного поля U в точці М₀, що належить заданій кривій, за напрямом цієї кривої.

$U=\frac{x}{y}-\frac{y}{x}$

$M_{0}(1;1)\in x^{2}+y^{2}-2y=0$

♦ $\frac{\partial U(M_{0}}{\partial l}=U_{x}^{'}\left(M_{0} \right)cos\alpha +U_{y}^{'}(M_{0})cos\beta =$

$U_{x}^{'}=\frac{1}{y}+\frac{y}{x^{2}}$

$U_{x}^{'}(M_{0}) = \frac{1}{1}+\frac{1}{1} = 1+1 = 2$

$U_{y}^{'} = - \frac{x}{y^{2}} - \frac{1}{x}$

$U_{y}^{'}(M_{0})=-\frac{1}{1}-\frac{1}{1}=-1-1=-2$

$f(x;y):\; x^{2}+y^{2}-2y=0$

$\begin{matrix} f_{x}^{'} = 2x & f_{x}^{'}(M_{0}) = 2 \\ f_{y}^{'} = 2y-2 & f_{y}^{'}(M_{0}) = 0 \end{matrix}$

$\vec{n}=\left\{f_{x}^{'}; f_{y}^{'} \right\}=\left\{2;0 \right\}$

$\left|\vec{n} \right|=\sqrt{4+0}=2$

$cos\alpha =\frac{2}{2}=1 \; cos\beta =\frac{0}{2}=0$

$=2\cdot 1-2\cdot 0=2-0=2$ .